
To any one who, for the first time, sees a great stretch of sandy
shore covered with innumerable ridges and furrows, as if combed
with a giant comb, a dozen questions must immediately present
themselves. How do these ripples form? Are they made and wiped
out with every tide, or do they take a long time to grow, and
last for many tides? What is the relation between the ripple
and the waves to which they owe their existence? And a host of
others too numerous to mention.
The questions to which I particularly directed my attention at
first were the following:—(1) How do the ripples first start?
(2) What is the relation between the water waves and the ripples?
During the course of this investigation certain fresh facts have
come to light, showing how the principles involved in the formation
of ripplemark apply to other phenomena of apparently widely
different origin. Some of these are included in the present communication,
but the discussion of others, less immediately connected with
ripples, I have deferred to a future occasion.
1. Starting of the First Ripple.—To the first question
as to the origin of ripplemark - fundamental as it
is - I could, for some time, find no satisfactory answer, either
in nature or in books. Even the deeply interesting paperb
in which Prof. George Darwin described the vortices he had discovered
in the water oscillating over ripplemark touched but lightly
on this point. Prof. Darwin said: "When a small quantity
of sand is sprinkled [in a glass trough] and the rocking begins,
the sand dances backwards and forwards on the bottom, the grain
rolling as they go.
"Very shortly the sand begins to aggregate into irregular
little flocculent masses, the appearance being something like
that of curdling milk. The position of the masses is, I believe,
solely determined by the friction of the sand on the bottom."
And again: "We now revert to the initiation of ripplemark.
"If the surface be very even, as when sand is sprinkled on
glass, when a uniform oscillation of considerable amplitude be
established, the sand is carried backwards and forwards and some
of the particles stick in places of greater friction. A
soon as there is any superficial inequality, it is probable
that a vortex is set up in the lee of the inequality which tend
to establish a dune there." [The italics are mine.]
With all the respect I felt for so eminent an observer-one, also,
who had thrown so much light on the subject - I could not concur
in this opinion. It seemed to me impossible that chance inequalities,
having no relation with one another, but scattered here and there
entirely without order, should develop into such ripples as are
commonly seen on the sea shore - straight as if ruled, all of the
same shape, and all at equal distances apart, or at distance
varying according to some definite law. I cast about, therefore,
for some other solution to the problem - some way of connecting
the ripples with one another from the beginning, without the intervention
of chance irregularities in the sand. I may say at once that I
have been successful in finding such a solution, and that I am
about to show how oscillating water can produce ripple-mark on
sand which is perfectly smooth and level to start with, and free
from irregularity of every sort.
My first experiments were carried out at Margate, with the rather
coarse brown sand found there. I tried oscillating water of variou
depths, over different thicknesses of sand, in vessels of all
sorts of shapes and sizes, from a soap dish some 4" x
3" x 2" to a
tank 44" x 18" x
18". 'The oscillations were produced by giving the
vessel either slight instantaneous horizontal pushes, or a very
small rocking motion, in time with the natural swing of the water,c
and by putting either rollers or cushions under the vessel to
ease the jerks. The sand was made quite level at the beginning
of each experiment, by being violently stirred up first, and then
gently and irregularly shaken while it was settling.
In every vessel ripples appeared in times varying from a few second to a few minutes; and in all those in which the water was simply made to rise and fall alternately at each end of the vessel, without the formation of intermediate waves, two things invariably happened:—(1) Ripples formed first across the middle of the vessel, a fact first observed by C. de Candolle,d and (2) after prolonged oscillation most of the sand had collected there also in a long ripple-marked heap, as shown in fig. 1 (Plate 3).

Since ripples formed first across the middle of the vessel, and as, also, the sand was gradually removed from near the ends to the middle, by prolonged oscillation, it seemed clear that it was the formation of a small ridgee across the middle, during the first few oscillations, that caused the ripples to start there first.
In order both to reduce surface friction, and to render observation
easy, I repeated the experiment, scattering a mere pinch of sand
as evenly as possible over the smooth bottom of a pie dish, some
8 inches long, containing about an inch of water. In this way,
each grain, being isolated from the next, could be easily moved
by the water, and as readily observed. The result was very striking.
After oscillation of the water for less than half a minute, the
whole of the sand was collected in a straight line across the
middle of the dish at right angles to the line of motion.
Scattering the sand again, and watching carefully how the water moved it, I saw that each swingf of the water pushed every grain that was being swept towards the middle farther than the next swing carried it away again from the middle. If a, for instance (fig. 2),
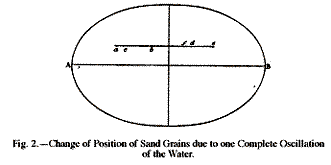
On the other side, during the same complete oscillation, a grain
at d would have been swept by the first swing to e,
and by the second, past d to f, so that this grain
also would have been moved towards the middle. Finally,
therefore one complete oscillation would have altered the distance
between the grains from a d to c f. In this way
all the grains very soon reached the middle line of the dish,
and remained oscillating over it as long as the motion of the
water was kept up.
It is clear that the formation first of the middle ripples, and
the collecting of a mound across the middle of the vessel after
prolonged oscillation could only be extensions of the operation
just described. This, then, is the way in which the first ridge
can form without the aid of any chance excrescence to start it.
When water is kept oscillating over sand, then, the dance of the
grains described by Prof. Darwin is not, as he conjectured, a
simple swaying to and fro, which would leave each grain where
it found it, but for chance inequalities of the surface. It
is, on the contrary, a steady periodic advance from
places where the horizontal velocity of the water is least to
places where it is greatest, each oscillation leaving the grain
nearer to their goal than it found them.
Since water which rises and falls alternately at each end of a
vessel, while its level remains nearly constant at the middle,
is really oscillating in a stationary wave, of which the middle
of the vessel is a loop, as regards horizontal motion, and the
ends are nodes, it is interesting to note that the sand, in gathering
across the middle of a vessel, is really collecting at a loop
of the stationary wave generated by the oscillation of the water.g
2. The Formation of Fresh Ripples beside an Existing One.—Having
established the primary ridge, and found the conditions necessary
for its formation from smooth and level sand, the next question
that arose was, how are all the other ripples started? Do they
depend for their initiation simply on unevennesses of the surface,
or are they also subject to some definite law? M. Forelh
noted that a foreign body in the sand set up, in some way
or other, a series of ripples in the sand on either side of it;
but how these ripples start - whether all at one instant or each
separately - and what is the process of initiation, has not, I
think, hitherto been elucidated.
The solution of the problem cost me several weeks of observation
and experiment, yet it was absurdly simple when it came. It wa
that a single ripple, existing alone, in otherwise smooth sand,
initiates a ripple on either side of it, that each of these ripple
produces another on its farther side—these in their turn originate
other ripples on their farther sides, and so on, till the whole
sand is ripple-marked. This suggestion having occurred to me,
I tried in many ways to make sure that it was correct. For instance,
I formed a fairly high ridge at some distance from the middle
of the vessel, and watched to see if others followed from that,
before the primary ridge in the middle became visible; or, again,
I made a ridge of some peculiar shape, such as this in plan, >,
and noted whether the succeeding ridges took the same, or nearly
the same shape; and they did, the angle in each one being more
obtuse than in that formed before it. Thus I felt sure of the
fact; it only remained to see how it was accomplished.
For this purpose I abandoned my brown sand in favour of silver
sand, which I had found to be so mobile that it spun in delicate
fairy-like vortices in the lees of some of the ridges. These
vortices, which differed widely from those discovered and described
by Prof. Darwin, were, as I afterward
found, the true ripple-forming vortices, and I therefore call
them ripple vortices.
3. Structure and Functions of the Ripple Vortex.—The vortice I saw had horizontal axes and were spiral in shape, and they seemed to scoop sand out from the bases of the ridges, and to push some of it up the ridges while they carried the remainder whirling round with them. In watching them it occurred to me that since each vortex (A, fig. 3)

In order to see if my surmise was correct, it was necessary to
simplify and magnify the action of the water, and also to see
its stream lines. To simplify it I used only enough sand to cover
the bottom of my glass trough (36" x
6" x 8"), and
I got rid of sand on the ridge by making an artificial ridge of
two china tiles sewn up in calico. To magnify the action, thi
ridge was made 2 inches high, and, so that no water should get
round it or under it, it fitted tightly across the trough, and
was jammed down on to the bottom.
Prof. Darwin employed ink squirted on to the sand to show him
the stream lines of the water; but, as I found that this was
impracticable with the violent motion necessary to raise sand vortices, I cast
about to find an insoluble powder that had only a slightly greater
specific gravity than water, so that it should move with the water
in all its twists and turns. I found that well-soaked ground black
pepper, after all the finest particles had been washed away, answered my purpose
perfectly. With this I was soon able to follow the exact course of the water under every kind of condition, and fig.
4 shows what happened during a swing from left to right when the
artificial ridge was in position, and when about a dessertspoonful
of pepper was in the water.
Soon after the water began to flow over the ridge a small vortex appeared on its right-hand side. As water continued to pour over the ridge the vortex enlarged, so that its centre moved farther away from the ridge; finally there was a large vortex as at A (fig 4),
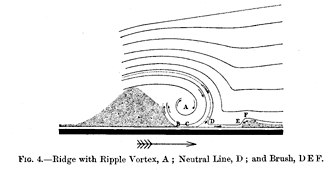
Since the water that strikes obliquely into the sand (DEF, fig.
4), after flowing over the vortex, clears a new furrow and sweep
up a new ridge exactly as a brush clears the floor and sweep
the dust up into a ridge, I shall call this water the" brush.''
The pepper, then, showed that the vortices and brushes cleared
out new furrows and swept up fresh ridges exactly as I had imagined
they did.
There are thus three ways in which sand ripples are originated,
viz., the "uneven surface" method, the "differential
motion" method, and the "brush" method. The first,
which was the one described by Prof. Darwin, could, unaided, give
rise to irregular ripple-mark only, since it consists in piling
up sand in places where the surface chances to be uneven. The
second is the method by which single ridges arise at the loop
of stationary waves. The third is that by which the brush of the
vortex in the lee of any existing dune or obstacle sweeps up a
new ridge beside it, leaving a hollow along the neutral line of
the vortex. The last two methods are evidently capable, unaided,
of originating and then extending regular ripplemark
wherever water is oscillating over sand, whether its surface be
smooth or uneven to start with. These last two, therefore, are
clearly the essential methods, while accidental unevennesse
of surface merely delay uniformity in the results.
4.The Origin of the Ripple Vortex.—Since the ripple vortex
with its neutral line and brush plays such a large part in the
initiation as well as in the growth of ripplemark, it i
clear that the causes of its formation and the laws of its development
must be traced before any satisfactory theory of ripplemark
can be evolved. It is, as is shown in fig. 4, a spiral vortex
composed of a ribbon of water wound round a cylindrical core,
just as the mainspring of a watch is wound round its barrel. And
one very curious fact that I observed about it was that it did
not come into play in the beginning, but only during the latter
part of each swing.
I had some difficulty at first in imagining how such vortice
could arise, and sought in vain among all the vast number of paper
on vortex motion that have been published within the last thirty
years for some light on the subject. These appeared mostly to
bear on vortices already formed, and moving in a frictionles
fluid of infinite extent. Few dealt with any real fluid, and
none, that I could find, with the process of formation of the
vortex. Prof. Darwin traced analogies between the rippleforming
vortices and those set up lay an oar in sculling, and by the motion
of a fish's tail; but nowhere could I find any suggestion as to
the actual process by which the vortices were generated.
Finally, I formed the hypothesis offered below, which is, I consider,
confirmed be the experiments on the early stages of ripplevortex
formation presently to be described. When the impulse is in the
direction AB, say (fig. 5), the water in the lee of a ridge,
DE, is more or less protected from the impulse by the ridge, and
therefore the water below D moves much more slowly than that above.
The first jerk of the impulse moves the water away from DE to
EF, say, and then friction between the quick and the slow water
enables the former to continue to drag the latter away from the
ridge, and thus to keep up the diminution of pressure between
DE and EF. The balance of pressure is, of course, immediately
restored by a flowing in of water from other parts. This diminution
of pressure in the lee of a ridge is one of the two necessary
conditions for creating a ripple vortex there.
To find the other condition we must consider where the water come
from that flows in between the ridge and the water in its lee,
when the pressure there is diminished.
In every mass of water oscillating about a single place of constant level, each swing distinctly divides itself into two parts - the first part (a, fig. 5), in which the higher half of the water falls, and the lower half rises to the average level; and the second part (b, fig. 5), in which that which was the higher half falls below, while that which was the lower half rises above the mean level. Thus, during every instant except the single one in which all the water is at the same level, the pressure exerted by every element of the water is compounded of two - one due to the velocity it has already acquired, and the other to the difference of level of the water at the moment. The second, which may be called "gravity pressure," is always, of course, exerted from the side on which the water is highest towards that at which it is lowest; and when there is a sudden attempt at a diminution of pressure at any one particular point, the direction of the gravity pressure at that point along each special line must be from the plane of highest level to the point. The gravity pressure at D, along the line PQ, for instance, when the pressure is diminished at D, must act from P towards D, and not from Q towards D, and similarly all the arrows in a and b (fig. 5)

The effect of the gravity pressure on the flow of the water, when
the pressure in the lee of a ridge is diminished by the drag exerted
by the flowing water on the still water, can now be readily traced
with the aid of fig. 5. The ridge is behind, and the water i
being pulled away from it in front, so that water to fill the
space can only flow from above or below. In the first part of
the swing (a, fig. 5) the water below D can clearly exert
no pressure along DE, anal therefore it is only that above D which
counts. This has a resultant gravity pressure along DE in a downward
direction, which must impart at each instant an additional downward
velocity to that which the water already possessed. Thus all the
forces acting on the water in the first part of a swing tend to
move it roughly in the same direction, and so no vortex then forms-the
moving water simply sweeps over the ridge, pressing as closely
as it can get against its lee side DE.
In the second part of the swing, when the water is highest on
the lee side of the ridge, matters are very different
— now the gravity pressure opposes the flow of the water,
and its resultant along DE evidently points up the ridge (b,
fig. 5), so that with a diminution of pressure at D the water
close to the ridge flows in the opposite direction to that at
a little distance from it, and so a vortex is created. Thu
the second condition for the formation of a ripple vortex is that
the resultant gravity pressure along the ridge on its lee side
shall tend upwards.
As a test of the correctness of the explanation suggested above
I studied some ripple vortices in water that was very shallow,
and that therefore moved extremely slowly. As, under these conditions,
pepper did not indicate the stream lines of the water with sufficient
delicacy, I had recourse to crystals of permanganate of potash,
each of which sent forth a steady stream of colour for several
minutes, which indicated the flow lines of the water with great
fidelity.
Insert Image
To ensure a slow motion of the water I had it less than an inch deep, and, in order that my eye should not be distracted by vortice in both directions, I arranged the trough as seen in elevation in fig. 6.
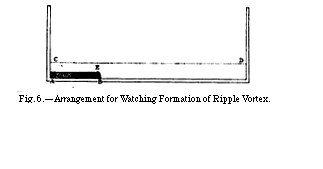
The following was the process of formation in the left to right swing. When the swing began, a thin straight stream of coloured water flowed over the ridge, obviously filling in the gap made by the moving away of the water that was nearest the side of the ridge (a, fig. 7, plate 3).i

There remained one further experiment to try in order to obviate
all possible doubt. If, as I had surmised, and as the above experiment
seemed to prove, it was necessary for the gravity pressure to
oppose the flow of the water for the vortices to form, then
no vortices of the kind I have described could be created by water
flowing steadily in one direction over an obstacle, for
in that case gravity pressure would always aid the flow of the
water.
In making this experiment I used a trough, A B (fig. 8),
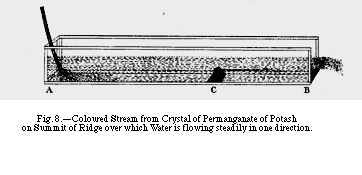
Closing the open end up to about twice as high as the ridge, so
that still water rested against the ridge, the stream of colour
from the crystal placed on the summit of the ridge flowed exactly
horizontally for distances varying between 1 and 2 inches, according
to the steadiness of the water, and then finished in a curiou
flickering motion. which is shown as nearly as possible in fig.
8j. Lowering the end barrier made no material difference
in the appearance of the coloured stream, but when it was completely
removed the rush of water flattened the sand ridge very considerably,
still leaving the lee side very steep, however, and then the surface
of the water was permanently lowered, and it rippled just beyond
the ridge, but no ripple vortices were formed.
Finding that no water streamed down the ridge when the flow wa
steady, I concluded that the friction between the flowing and
the comparatively still water was not sufficient to move the latter
under steady conditions, but that a jerk was required to overcome
the inertia of the stiller water. To try if this were so I gave
the flowing water an impulse by pushing it along towards the ridge
with a slip of wood the width of the trough. The result was that
a small stream of colour immediately appeared against the side
of the ridge, and, as soon as the water in front of the ridge
rose higher than that behind, a vortex formed.
These experiments appear to me to prove conclusively that the
creation of ripple-forming vortices depends entirely upon the
two conditions I have formulated, viz.: (1) the establishment of
a diminution of pressure in the lee of an obstacle; and (2) the
turning down and back again of the water that has flowed over
the ridge, through the backward pressure on it of the water that
is temporarily raised above the main level in the far end of the
vessel.k Thus ripple vortices depend for their existence
on variations in the gravity pressure of oscillating water that
obviously must exist, but the importance of which in connection
with the formation of vortices has not, perhaps, before been recognized.
It has hitherto been supposed that a uniform steady current of
sufficient velocity was capable, unassisted, of generating vortices,
both of the sand—raising type and of other types, when flowing
over an uneven sandy bottom. My experiments given above, and other
that I hope to publish later, show, however, that although the
water in the lee of an obstacle over which there is a steady flow
is disturbed, no definite vortex in the least resembling a
ripple vortex forms there. Hence a steady current is unable either
to generate or to maintain ripple-mark.
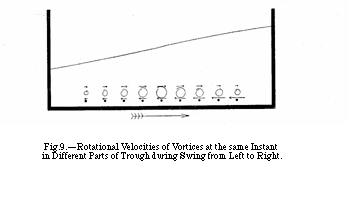
5. Different Intensities of the Ripple Vortices.—The ripple
vortices have not all the same intensities, and at the ends of
the vessel they even differ so widely on the two sides of the
same ridge that the vortex facing the middle of the trough in
one swing is incapable of moving the sand, while the end-facing
one in the next swing raises a pretty little sand vortex. A little
consideration shows that this must be so.
Ripple vortices are caused by a current flowing over the summit
of a ridge away from its lee, acted on by a pressure exerted
towards the lee. The rotational velocity of the vortex must
depend upon the horizontal speed of the current and the magnitude
of the pressure combined.
Now the horizontal velocity of the current increases from zero at the near end of the vessel (the end at which the impulse i given) to a maximum at the middle, and diminishes to zero again at the far end. Hence, if the nine dots in fig. 9
6. Initial Ripple-distance.—Prof. Darwin observed that
the ripple-distance increased with the number of oscillation
of the water after its initiation, but, in the absence of any
information as to the process of initiation, it has been impossible
for any one hitherto to judge of what determines the first distance
of one ripple from another. We can now, however, ascertain thi
from a consideration of the laws governing the lee vortex and
its brush.
In smooth and level sand with a single ridge in it, the first
swing of the water causes a vortex to form in the lee of thi
ridge, the brush of which sweeps together a line of sand that
is the nucleus of a new ridge (fig. 4, p. 290). Clearly the distance
between this new ridge and the old one is determined by the final
size of the vortex in that first swing and the distance between
its neutral line, D (fig. 4), and the new ridge, EF, which distance
I shall call the sweep of the brush. As this latter is the more
important factor of the two in determining the ripple-distance
I shall deal with it first.
The Sweep of the Brush.—The sweep of the brush depend
upon two things, viz., the velocity of the water that forms it
and the room it has to spread in. From the nature of the brush
its velocity must vary with the horizontal velocity of the water
passing over the ridge, and this is greatest in the middle of
the vessel, greater the greater the amplitude of the wave, and,
since the horizontal velocity varies less, in different part
of the vessel, the deeper the water, the sweep of the brush also
varies less, in different parts, the deeper the water.
The room the brush has to spread in evidently depends, not only
upon the length of the trough and on where the generating ridge
is in the trough, but also upon whether the vortex is on the end-facing
or the middle-facing side of the ridge. Thus the sweep of the
brush is greater—
The Size of the Vortex.—As the vortex is a band of water
wound round a cylinder of originally stiller water, its size at
any given instant is greater the larger the cylinder is to start
with, the more quickly it is wound and the longer it spins.
Now the thickness of the cylinder to start with depends on the
height of the generating ridge, within certain limits to be determined
later. The velocity with which it is turned has been shown to
depend on the horizontal velocity of the water that rubs the sand,
and on the backward gravity pressure, both of which are function
of the amplitude of the wave and of the position of the vortex
in the trough and on the ridge. The duration of the vortex depend
upon the periodic time of oscillation, which bears a direct relation
to the length of the trough and is an inverse function of the
depth of the water.
The vortex is larger, at any instant, therefore—
The conditions necessary for the vortex to be large, then, are
very similar to those required for the brush to have a long sweep,
except in one particular—the vortex is larger on the endfacing
side of the ridge, and the sweep longer on its middlefacing
side. When two conditions are at war, experiment must prove which
gets the upper hand. I used my artificial ridge to try this, and
found that the new ridge created on its middlefacing side
was always farther from it than the one created on its endfacing
side, but that the two distances differed less the nearer the
artificial ridge was to the middle of the vessel.
We can now, by combining the conditions necessary for the vortex
to be large with those requisite for the brush to have a long
sweep, find out how the initial rippledistance varies with
varying conditions. This distance must increase with—
The two limits mentioned above are the following:—
(1) If the first ridge is so high that the velocity of the water
is only sufficient to move a small portion of the slack water
in its lee, the diameter of the cylindrical core is determined
by the velocity of the water instead of by the height of the ridge.
In that case the new ridge rises on the first one instead
of beyond it.
(2) When the water is so shallow that its friction is insufficient
to move the particles of sand, no ripples form.
7. The Growth of Ripple-mark.—Let BCD (1, fig. 10)
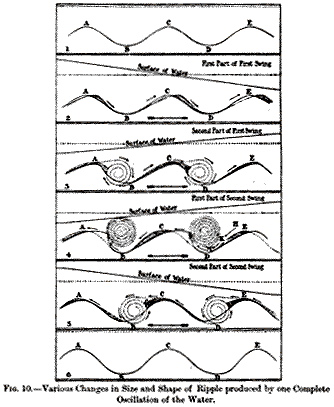
In a swing, from left to right, say, at the first instant no vortex
forms on either side of BCD, sand is simply pushed up BC, and
a little is washed off the summit C, and thrown or dropped anywhere
between C and E. (2, fig. 10). Next a vortex forms against CD,
which is made apparent, if the motion is strong enough, even without
the use of pepper, by the whirling round of the sand scooped out
by it from the lower parts of CD (3, fig. 10), and by the movement
of the sand up DC against the general flow of the water. At the
same time sand continues to be pushed up BC to the summit, where
a part of it rests, while the remainder slides over to the other
side, and, being kept from falling by the vortex, gathers into
a small ridge such as F (3, fig. 10). Then when the swing changes,
the sand in the vortex rises, spreading out as it goes (4, fig.
10). The part of this sand that touches the summit C remains there,
and the rest is carried along to the left, to a distance varying
between a fraction of an inch and several inches, according to
the horizontal velocity of the water and the periodic time of
the oscillation. Wherever this vortex has reached when the swing
changes, all the sand that has not fallen by the way is deposited,
unless the motion is so violent that some is carried back again
in the next swing, before it drops. The first flow of the water
in the new swing also sweeps the ridge F up to the summit and
leaves it there (4, fig. 10), so that this helps to raise the
summit. After this a vortex forms against BC (5, fig. 10) as it
did previously against CD, and at the end of the swing the ripple
resembles BCD (5, fig. 10), B being lower and C higher than in
3 (fig. 10). Thus every swing raises the summit and lowers the
base of the ripple and so increases its height doubly. When the
oscillations are allowed to die away, the small ridges at F and
G raised by successive swings are smaller and higher up with each
oscillation, till, when the water comes to rest, the ripple resemble
6 (fig. 10), C being higher and B lower than when the oscillation
started.
All this is what is seen when ripples are growing under
oscillating water. The explanation of most of it is obvious,
from what has gone before. The first instant of observation, during
which no vortex forms, is what I have called the first part of
the swing—the time when the water is gaining its mean level,
and there is, consequently, no backward gravity pressure. The
next moment, when the sand vortex forms, is what I have called
insert image source
the second part of the swing, when the water is rising above it
mean level, and there is, therefore, a backward gravity pressure.
The only part of the operation that has not already been accounted
for is the expansion and rise of the vortex when the swing changes.
This I explain in the following way:—
The vortex is formed and grows under pressure from the onward
flowing water above and the backward pressed water below. At the
moment when the swings changes, the water as a whole comes to
rest, with the result that the downward pressure of the flowing
water is taken off the vortex, while the upward pressure from
the raised water remains, (HKM, 4, fig. 10). The moment the downward
pressure is taken off, the vortex expands, I imagine owing to
its centrifugal force, and is raised upward by the pressure of
the high water, and it is then swept onward in the new direction
with the new swing.
8. The Motion of each Ripple as a Whole.—Concerning the
growth of the rippledistance, Prof. Darwin says: "On
the parts of the plate where the sand is thick, a continual rearrangement
of ripple-mark goes on ; the wavelength extends by the excision
of short patches of intercalated ripplemark, and by general rearrangement.
Finally, the sand reaches an ultimate condition as regards wave-length,
although rearrangement of ripple-mark still appears to go on for
a long time."
My own earlier observations apparently accorded with this description, but, wishing to find out more definitely exactly the rearrangement took place, I started de novo with smooth level sand, in the middle of which I had artificially made two ripples as starting points for other ripples. These were raised by pressing a thin slip of wood down into the sand and then withdrawing it, after moving it slightly to each side, to pile up the sand (a, fig. 11, Plate 4).

After a few oscillations, each of the ridges (b, fig. 11)
was half an inch or so farther from the middle of the vessel than
at starting, while the two new ridges that one would have expected,
from what has gone before, had formed to the left and right of
them.
Further oscillations increased the spaces between all the ripples, as well as producing more ripples to the right and left of them (c, fig. 11). Thus, for a short time after its initiation, each ripple travels farther from the one that generated it, and, consequently, from the middle of the vessel, with every oscillation. After a little while - some time before the whole of the sand wa rippled - the summits of the two ridges that were nearest the middle of the vessel first became stationary, and then began to move back towards the middle with each oscillation. Next the same thing happened to the next ridge on either side of the middle ones, and finally - soon after the whole of the sand had become ripple-marked - all the ripples were travelling towards the middle of the trough. Now it is obvious that if all the ripple travel towards the middle of the vessel, at least two of them must at last coalesce, and then two others, and so on; and thi does actually happen. As soon as two ridges get so close together that the vortex of one can snatch sand from the summit of the other, while that other, from inferiority either of size or position, or both, is incapable of returning the compliment, thi second one quickly gets swallowed up, and its sand goes to swell its rival These coalitions generally take place at or near the middle of the trough, and they would naturally always do so but that the sand, water, and impulses are never perfectly symmetrical. For the same reason the whole length of a ripple seldom gets absorbed at the same time. It is usually higher in one part than in another, and then the lower part disappears first, while sometimes the higher joins on to the demolishing ripple that is on its endfacing side, as shown in plan in a, fig 12,

For some little time after the whole sand has become rippled,
in a trough, the ripple-distance at the ends is only slightly
less than at the middle; but as the height of the middle part
of the sand grows, while that of the ends diminishes under continued
oscillation, the ripple-distance increases in the middle
while it diminishes at the ends, so that at last the series of
ripple-distances is graduated from very small - perhaps half an
inch or so at the ends of the vessel to three or even four inche
in the middle. All these changes of ripple distance are entirely
effected by the coalition of ripples just described, together
with the formation of new ripples at the ends of the trough, and
these two phenomena are due to the motion of the ripple
as wholes, which is brought about in the following manner:—
It is easy to see that the motion must be connected with the transference
of sand from one side of a ridge to the other and back again during
each oscillation (fig 10, p. 301). If more sand were always deposited
on the right side in one swing than was swept back on to the left
side in the next, for instance, the middle plane of the ridge
would travel from left to right, and the whole ridge would therefore
do likewise; and, vice versa, an excess of sand placed
on the left side would lead to the motion of the ridge from right
to left. I shall now show that this unequal transference of sand
is exactly what must take place among a series of ripples.
It has been seen that during the second part of a swing (3, fig.
10) a vortex scoops up sand FD from the lower part of one side
of a ridge, and that during the first part of the next swing it
carries this sand over to the other side of the ridge, together
with a slice of sand which it cuts off from the upper part of
the first side (4 and 5, fig. 10). The amount of sand scooped
out by the vortex is greater the larger and swifter the vortex;
also the slice of ridge carried over the summit with the vortex
sand increases with the depth of the side of the ridge and with
the longitudinal velocity of the water, and is greater when thi
velocity is increasing than when it is diminishing.
Now, I have shown that in established ripple-mark, the end-facing
vortex of a ridge is always larger and swifter than its middle-facing
vortex. Also, the flowing water has always an increasing longitudinal
velocity when it is washing sand from the end-side to the middle-side
of a ridge, since it is then travelling towards the middle
of the vessel, and a diminishing velocity when it is carrying
the sand in the opposite direction, away from the middle. It follows,
therefore, that in established ripple-mark, more sand must be
transferred from the end-side to the middle-side of a ridge in
one oscillation than is conveyed back again to the end-side in
the next oscillation, and it is for this reason that the ridge,
as a whole, travels towards the middle of the vessel. In fact,
each established ripple partakes, as a whole, of the general
movement of the sand towards the places where the longitudinal
velocity of the water is a maximum. It is thus apparent that,
unless there is little enough sand for it all to collect at the
middle, the ripples must continually re-arrange themselves, not
only for a time, but for as long as the oscillation is continued,
or till the sand is piled up in such a way that ripples are no
longer possible.
The apparently anomalous cases when the ripple moved away from
the middle are readily explained. These were: (1) when the first
two ripples were made by pressing a slip of wood down into the
sand in the middle of the vessel, so that the furrow between the
ridges was deeper than the furrows on their other sides (a,
fig. 11); and (2) when a new ripple was generated by the end-facing
vortex of an existing one (c, fig. 11, Plate 4). Both these
ripples had deeper middle-side than end-side furrows - the first,
because it was specially made in that way, and the second, because
the vortex on the middle-facing side of the ridge had scooped
out the furrow below the mean level of the sand, whereas no vortex
had yet existed on the end-facing side, which was merely a small
pile swept up above the level of the sand (b, fig. 11).
Hence, at first, the end-facing vortex of each ripple was smaller
than its middle-facing vortex and the end-side of the ridge wa
shallower than its middle-side, for both of which reasons les
sand was at first scraped off the end-side of the ridge in one
swing than was returned to it, from the middle-side, in the next;
and, consequently, the ridges travelled endwards. As, however,
the end-facing vortex has always a greater rotational velocity
than the middle-facing vortex (see p. 297), the end-side furrow
deepened more quickly than the middle-side one. Hence, the disparity
in the quantity of sand that was scraped off each side alternately
gradually disappeared, and when this became equal the ridge became
stationary. As the end-side furrow still continued to deepen more
rapidly than the middle-side one, however, more sand wa
now scraped off the end—side than was returned to it, and so the
normal state of things was brought about, viz., the ridge travelled
as a whole towards the middle of the vessel.
In order to test the validity of the foregoing argument, I made
two ripples in the middle of the vessel by scraping up sand from
both ends, and then pressing down the slip of wood into the middle
of the resulting dune, so that the end—sides of the two ripple
thus formed were longer than their middle-sides. The result wa
as I expected. After a few oscillations, instead of the two dune
having separated further, they had coalesced and become one, through
each having moved towards the middle.
Other experiments of the same kind such as making a ripple about
halfway between the end and the middle, and first having its deeper
furrow on the end-side, and then on the middle-side, were equally
successful; for, in the first case, the ripple moved towards the
middle, and in the second, towards the end of the vessel.
9. Side of Ripple facing Shore Steeper than Side facing Sea..—The
unequal sizes of the vortices on the two sides of a ridge and
the unequal transference of sand from one side to the other naturally
affect the shape of the ripple. The larger end-side vortex hollow
out a deeper end-side furrow, tending to make the end-side of
the ridge steeper and deeper than the middle-side, a tendency
that is strengthened by the greater transference of sand to the
middle-side, and that is still further accentuated by the sand
dropped by the travelling vortices, which naturally rests more
easily on the gentle slopes than on the steep ones (fig. 1, Plate
3). This is the reason that the ripples on the sea shore generally
have steeper slopes facing the shore and gentler slopes facing
the sea. The shore takes the place of the end of the vessel in
checking the flow of the water, so that the shore-sides are the
end-sides of the ripples, and the sea-sides are what I have called
their middle-sides.
10. The Longitudinal Markings of Rippled Sand.—Sand ripple are never entirely smooth, they are marked with small irregular longitudinal ridges and grooves, almost as if they had been combed (fig. 13),
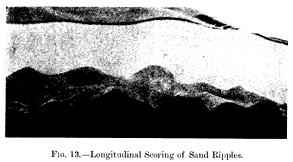
During their growth they have to sustain the weight of such ridge
as those marked F (fig. 10, p. 301). But from accidents of slipping
this ridge has very varying weights in different parts. Where
the weight is heavy, the sand slips further, and the vortex i
necessarily smaller than where it is light. Hence, each vortex
is not single, but is composed of a series of vortices of different
diameters set end to end.
When the swing changes, the series breaks up into a number of
separate small vortices, each having its axis inclined to the
horizontal at some angle that depends upon the contour of the
sand against which it was twirling at the moment when the swing
changed, and it was pushed back and up. The inclination of the
axis to the horizontal is sometimes so great that it actually
becomes vertical, and but few of the vortices remain horizontal
after they have begun to travel.
11.Travelling Vortices.—We have now traced three step
in the advance of the sand from the ends to the middle of the
vessel:—
There remains one more step to complete the series. When the vortice
are carried away from their generating ridges, after each new
swing, it is the large vortices from the end-facing side
of the ridges that are transported towards the middle of the trough,
while the small ones from the middle-facing sides are taken
in the opposite direction. The sand that is continually dropping
from them, therefore, falls more thickly on the middle of the
vessel than on its ends, so that in this way also the gathering
of the sand in the middle is accelerated. Thus, every operation
performed by the water—except one which is purely temporary—tend
to drive the sand from the ends to the middle of a vessel, when
it is oscillated in such a way that the water level remains constant
in the middle, and has its maximum variations at the ends. No
wonder, then, that the sand soon becomes banked up in the way
shown in fig. 1.
12). Ripple-Mark on the Sea-Shore.—For the ripple-mark
that I have hitherto considered, one of two conditions was necessary
to start the ripples. Either the oscillating water had to have
at least one constant place of maximum longitudinal velocity,
or there must be at least one obstacle or hollow in the sand to
give birth to vortices. Of obstacles in the shape of stones, bunche
of seaweed, etc., as well as of hollows, there is generally no
lack on a sandy shore, But the question arises—would a beach that
was entirely smooth and featureless to begin with become ripple-marked
when the sea oscillated over it? Obviously it would, for in order
to start a primary ripple it would only be necessary for the water
to have a maximum longitudinal velocity at or near the same place
few successive oscillations, so that even a single one of the
smallest of small primary ripples could form. Once this was done,
other ripples, as I have shown, would arise as a matter of course,
until the whole sand was covered with ripple-mark; and the ripple-mark
would be very regular, for although the places of maximum horizontal
motion of the water would often remain the same, or nearly the
same, for a short time, yet they would not usually remain so long
enough for such mounds as those shown in fig. 1 to form. On the
contrary, the velocity and back gravity pressure of the water
flowing over any individual ripple must be continually changing,
so that on the average each is subjected to the same influences,
and their heights and ripple-distances are therefore fairly equal
after any single tide. But as the heights and ripple-distance
of all vary with the amplitude of the wave, they are greater after
a storm than during calm weather.
In order to try and imitate the action of the sea on an originally
smooth sandy beach I used about an inch of sand made quite smooth
and level in my 36-inch trough, with about 2 inches of water above
it. I then alternately raised and lowered one end of the trough,
bit by bit, giving it a slight jerk at each rise or fall, to make
the water oscillate, but allowing several oscillations to take
place between each jerk. In this way not only did the place of
maximum longitudinal motion differ slightly for each oscillation,
but the depth of the water changed at the same time, which i
exactly what happens in the sea. When this was done for some time,
the sand remained level on the whole, but became covered with
very regular even ripple-mark, just like that of the sea-shore
and, as was to be expected, the sand did not rise higher, on
the whole, in any one place than in any other.
It might be objected that, since all the conditions for the formation
of ripple-mark appear to exist in every place where there
is a sandy beach washed daily by the tides, ripples ought to be
much more universal in such places than they are. The reply i
that they are universally made, but that most of
them get smoothed out by the edges of the waves of the retreating
tide, and only remain intact in pools or depressions of any kind,
where the water, being temporarily left by the retreating tide,
sinks slowly and uniformly downwards through the sand.
13. Ripple-Mark under Stationary Waves.—In my earlier experiment the trough was oscillated in the simplest possible way, i.e. so that the length of the stationary wave was twice the length of the trough. Subsequently it occurred to me that by oscillating more quickly I ought to be able to get smaller stationary waves, the effect of which on the sand would be to produce groups of ripples at or near the loops of the waves, where the longitudinal velocity was a maximum, and to leave smooth spaces at or near the nodes, where it was a minimum. In this I was successful, and fig. 14, Plate 4,

The height to which a mound can rise when the water has a given
minimum depth and the quantity of sand is practically unlimited
depends solely on the length of the stationary wave.This.wave-length
settles the distance between the mounds, and this distance determine
the height to which a mound will rise before some of it slip
down, or before the weight of the highest part makes it spread
out laterally, thus partially filling up the space between it
and the next mound, and so diminishing its height again.
The following is what happens when oscillation is prolonged:—If
the sand is thin, it collects in separate mounds at the place
of maximum longitudinal velocity, leaving the bottom of the vessel
bare between. If the sand is of practically unlimited thicknes
it rises to a certain height at each of such places, and then
broadens on the top into a sort of tableland, smooth at first,
but covered with irregular ripple-mark afterwards. When this happens,
the mound has reached the maximum height it can attain to under
the given conditions. Soon sand slips, somewhere, and the whole
shape changes somewhat, and then rebuilding goes on, till the
same height is reached again, and then another slip occurs—sometime
two or three in different places—and rebuilding starts afresh.
There is thus no exact height which the mound retains,
but it has a maximum height for each wave-length, provided
the water has a certain minimum depth above the top of the mound
when it is at its highest. Increased amplitude of the wave hasten
the attainment of this height, while greater depth retards it;
but nothing but a change of wavelength alters it,
I think.
When the oscillation is very regular, the bare spaces between
the mounds remain entirely free from ripple-mark, as in fig. l4,
Plate 4, but if it is at all irregular, there are no parts of
the sand where the level of the water remains quite constant,
and then a series of ripple-marked heaps rise which are separated
by no smooth spaces.
In shallow water after a time, the tops of the mounds become flat,
and the furrows then look like grooves cut for irrigation purposes.
In one case, for instance, the mounds finally became quite flat-topped,
with runlets between, as shown in profile in fig. 15.
The process described above, by which mounds of sand are built
up under the action of stationary waves, may be summarized a
follows:—
After having arrived at the above conclusions, and proved them
experimentally, I found that C. de Candolle,l in a
long and most interesting paper on the subject, had mentioned
that, under stationary waves, he had observed groups of ripple
with smooth spaces between. He said: "Lorsqu'il existe dan
l'auge plusieurs ondes stationnaires, il se forme autant de système
de rides qu'il y a de ces ondes" (this would only be correct
if C. de Candolle used the term "onde" to signify a
half of what we call a stationary wave). He continued: "Et
ces rides sont groupées de part et d'autre de chaque
plan vertical séparant deux ondes contiguës."
[The italics are mine.] This appears to be vague, but the context
shows that C. de Candolle meant the places of constant level,
and it is, therefore, a true description. He appears, however,
to have failed to notice the most important point about these
groups of ripples, namely, that they finally grew into mounds,
nor do I think that this fact has ever been previously mentioned.
With regard to other mounds formed by stationary waves, I should
suggest that the tidal sand ridges first discovered by Prof. Osborne
Reynoldsm in his model westuary were thus produced,
and that the similar ridges to be found in natural estuaries,
many of which Dr. Vaughan Cornish has so ably described and beautifully
photographed, have a like origin.
Besides tidal ridges, it seems probable that the chains of sand
banks in the sea and of sand dunes on shore, as well as the gigantic
sand heaps in the Asiatic deserts described by Sven Hedinn
; originate and grow under the action of waves that are stationary
for longer or shorter periods, while the smaller ripples that
cover all of them are due to vortices similar to those that I
have shown to produce the ripple-mark of the sea-shore.
References
a. Publication postponed by author's desire until June, 1910.
b. "On the Formation of Ripple-mark in Sand," 'Roy.
Soc. Proc.,' November 22, 1883, vol. 36, p. 23.
c. When each impulse is prolonged, even although the impulse
be in time with the natural vibration of the water, the effect
on the sand is quite different, for a reason that will be given
in another paper.
d. "Rides Formées à la Surface du Sable
Déposé au Fond de l'Eau," Archives de
Sciences Physiques et Naturelles,' Periode 3, vol. 9, p. 253 (1883).
e. I use the word "ridge" to define an elevation, and
a "ripple" to mean a ridge and furrow combined.
f. I call each travel of the impulse from one end of the vessel to
the other a "swing," so that there are two swings to
each complete oscillation.
g. The terms "loop" and "node" have a perfectly
definite meaning when applied to a vibrating string, for example,
and mean the places of maximum and minimum motion. But when applied
to a fluid oscillating with stationary waves, the terms are apt
to be misleading, since in the first place where the vertical
motion is practically zero the horizontal motion is a maximum,
and where the horizontal motion is practically zero the vertical
motion is a maximum. Hence the node for vertical motion is the
loop for horizontal motion, and vice versâ.
h. 'Archives des Sciences Physiques et Naturelles,' Periode 3, vol. 10, p.39.
i. The end of the barrier and the water near it only are shown in
the photograph.
j. It is impossible to give an exact representation of this motion,
because tiny water ripples came and went and flickered almost
like the flame in a coal fire, which is now in one place, now
in another.
k. I am aware that this explanation has been contested, and I
offer it entirely on my own responsibility.
l. "Rides Formées à la Surface du Sable
Déposé au Fond de l'Eau," 'Archives de
Sciences Physiques et Naturelles,' Période 3, vol. 9, p. 253 (1883).
m. First Report of Committee on the Action of Waves and Currents,"
'Report of the British Association,' 1889.