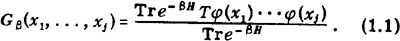PHYSICAL REVIEW D VOLUME 9, NUMBER 12 15 JUNE 1974

Symmetry behavior at finite temperature*

L. Dolan and R. Jackiw

Laboratory for Nuclear Science, and Department of Physics,
Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
(Received 18 March 1974)
Spontaneous symmetry breaking at finite temperature is studied. We show that for the class of theories discussed, symmetry is restored above a critical temperature. We determine this by a functional-diagrammatic evaluation of the effective potential and the effective mass. A formula is obtained in terms of the renormalized parameters of the theory. By examining a large subset of graphs, we show that the formula is accurate for weak coupling. An approximate gap equation is derived whose solutions describe the theory near the critical point. For gauge theories, special attention is given to ensure gauge invariance of physical quantities. When symmetry is violated dynamically, it is argued that no critical point exists.

I. INTRODUCTION

By drawing an analogy with the Meissner effect, Kirzhnits and Linde1 have suggested that spontaneous symmetry violation in relativistic field theory will disappear above a critical temperature. They gave qualitative arguments to support this contention in a theory with global symmetry (not a gauge theory) and obtained an order-of-magnitude expression for the critical temperature in terms of the parameters of the theory. This problem was next examined by Weinberg, who, in a preliminary investigation,2 derived a numerical value for the critical temperature in the Kirzhnits-Linde model. He then began to develop a complete analysis of spontaneous symmetry violation and/or persistence at finite temperature, with special emphasis on gauge theories with local symmetries.

It was Weinberg who suggested to us that the diagrammatic-functional method for evaluating effective potentials in field theory, which had recently been developed,3-5 might be profitably employed to study temperature effects. We report here the results of our investigation. Weinberg has also presented an analysis of the problem.6 He uses diagrammatic methods to determine a temperature-dependent mass, as well as operator techniques to compute a temperature-dependent potential. We give a functional-diagrammatic evaluation of these quantities, from which the critical temperature can be deduced. All physical results are in agreement and confirm the qualitative observations of Kirzhnits and Linde.1

We examine a field theory at nonzero temperature, or equivalently the ensemble of finite-temperature Green's functions, defined by


--------
See article in journal for remaining text.