Physical Review, Series 1, 18:135(1904).
Proceedings of the
American Physical Society
Minutes of the 21st Meeting
A regular meeting of the Physical Society was held in Fayerweather Hall, Columbia University, New York City, on Saturday, October 31, 1903, President Webster being in the chair.
The following papers were presented:
On the Nature of Certain Radiation
from the Sulphate of Quinine
By Fanny Cook Gates
When the sulphate of quinine is either heated or cooled through a high range of temperature, it is known to become temporarily phosphorescent and to possess the power of discharging an electroscope. It has been thought by some that this phenomenon, resulting from simple chemical reactions, is an argument for attributing the radiations of radium and the other active minerals to purely chemical changes. To obtain evidence in favor of or against such a view, experiments were made ascertaining the nature of the radiation given off by quinine sulphate under the conditions named, and a comparison made between their characteristic properties and those of the radiation from the radioactive substances. The quinine was sifted uniformly over a metal plate and heated to a known temperature, immediately after which it was placed in a testing vessel between parallel electrodes one of which was joined to the quadrants of an electrometer and the other to the pole of a storage battery, other connections being made as usual. Here it wa allowed to cool to a known temperature and the total amount of radiation emitted by the quinine during a given change in temperature was measured by the quantity of electricity discharged through the electrometer. By changing the range and the rate of cooling and the strength and direction of the electric field, curves were obtained showing the exact effect of such variation on the resulting radiation. The absorption of the rays in air and in other substances was also tested.
Unlike the radiations from the radioactive substances, which are incapable of alteration through any change in temperature and appear not to vary with time, the radiations from quinine sulphate are only apparent when accompanied by a great change in temperature. They vary in intensity during this change and in a short time they cease altogether. By increasing the strength of the electric field it is impossible to secure a maximum ionization current from the quinine radiations although a saturation current is readily produced with the radiations from radium, thorium and uranium. The quinine radiation are completely absorbed by a very thin sheet of aluminum and are largely absorbed by two or three millimeters of air and probably by less, which is in marked contrast to even the least penetrating rays of the active elements. Another striking difference in the behavior of the two types of rays i that those from quinine undergo a change in intensity when the direction of the field is changed. When the lower electrode on which the quinine rest is joined to the positive pole of the battery the resulting current is invariably larger than when it is joined to the negative pole.
The variation of the current with electromotive force is very similar to that obtained when ultraviolet light falls on a charged surface except that both positive and negative ions are present. The difficulty in obtaining saturation is doubtless caused by the fact that the ionization takes place very close to the surface of the quinine and that the ions rapidly diffuse to its surface and cannot be removed without a very intense field. The difference in the positive and negative current is probably due to a difference in the size of the positive and negative ions, the positive ions traveling faster than the negative ones; and the difference in size may be explained by the condensation of vapor around them in the same way as the increase in the size of the ions in flame gases when the gases cool.
The effect appears to be due to some type of radiation which is rapidly absorbed in the gas, and since the electrical effects are accompanied by marked phosphorescence it is possible that the ionization is caused by very short waves of ultraviolet light, such as Lenard has shown to be active in ionizing the gas.
These considerations give no evidence for believing that the ionization is due to projected bodies and make it appear certain that the ionizing action of quinine is caused by molecular actions which are influenced by temperature, and not by the spontaneous projection of charged masses from the atom, as in the case of radioactive bodies.
The Theory of the Electrodeless Discharge
By Bergen Davis
The theory of the discharge developed is derived from and explains some direct experimental data on the number of volts per centimeter required to produce the electrodeless discharge in gases at various pressures.
The electrodeless discharge was produced by the discharge of a Leyden jar system, which system was charged by the secondary of an induction coil giving 180 discharges per second. The spark gap in the secondary was adjusted until the white discharge just appeared in the vessel.
The volts per centimeter acting around the vessel were directly measured by a coil of five turns of wire of a diameter slightly less than that of the vessel. This coil was connected to a micrometer spark gap. The coil that had produced the discharge was lowered over the coil, and the micrometer spark gap adjusted till a spark passed. The potential at this spark gap divided by the length of wire in the measuring coil gave the volts per centimeter acting around the vessel.
Two frequencies of oscillation of the Leyden jar system were used. Let T1 and T2 be the time of a half oscillation for the two frequencies, then:

The results obtained were as follows:
Experiments were made in air, carbon dioxide and helium. The potential gradients obtained for air are shown in curves in Figure 1 and Figure 2.
The curves for pressures above the critical are nearly straight lines. They have the equation:
| X = cp + d | (1) |
The curves of the pressures below the minimum are equilateral hyperbolas, having equation:
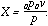 | (2) |
The ionization is taken as due to impact of other ions. Consider that when the discharge appears, there are N ions present, and before the application of the force there are N0 ion in a unit volume of gas. Then during a halfoscillation the ionization build up from N to N0 ions, according to the equation:
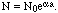 | (3) |
Where a = log b, and b is the number of ions produced by one ion at each impact including itself. a is the number of successive impacts in T, the time of a half oscillation.
It is assumed that N and N0 vary in such way that N/N0 = constant for any pressure, then, aa = constant.
The mean path of an ion, will be traversed under
a force X in time t according to:
of an ion, will be traversed under
a force X in time t according to:
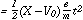 | (4) |
But a = T/t, since a is the number of times that the ion go through their free path in time T. Consequently:
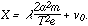 | (5) |
v0 in equations (4) and (5) represents the total amount of the electrical intensity that is consumed by the delay of the ions after each impact. This quantity v0 is found to vary inversely as the pressure, that is:
 .
.Hence (5) becomes:
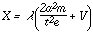 | (6) |
Equation (6) is the complete equation for the discharge at pressures below the critical pressure. The constant V is the displacement of the equilateral hyperbola along the axes of coordinates. It is the point of intersection of line (abg) in Figure 2, with this axis. In air it has the value of 4.4 volts.
The electrical intensity at pressures above the minimum is independent of
the frequency of oscillation. I he condition to be satisfied is that the
electrical intensity X shall be such that Xe is a constant and
equal to w, the energy of ionization by impact. The equation of the
discharge at pressures above the critical pressure i
is a constant and
equal to w, the energy of ionization by impact. The equation of the
discharge at pressures above the critical pressure i
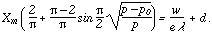 | (7) |
The left member of this equation represents the departure of the observed curve from a right line. This departure is due to the fact that the applied potential is a harmonic one. At large pressures, the crest of this potential only is effective, while as the critical pressure is approached, the effective force lasts throughout nearly the whole harmonic half oscillation.
The measuring instrument measured the maximum of this varying potential. Hence:
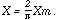
At pressures above the critical point the controlling condition of the discharge
is that Xe . shall attain the value w.
At pressures below the minimum (critical) point, the energy Xe
. shall attain the value w.
At pressures below the minimum (critical) point, the energy Xe exceeds the value w very much. The controlling
condition here is that the ionization must attain the density N for
the appearance of the discharge. The critical point occurs at he intersection
of these two controlling conditions.
exceeds the value w very much. The controlling
condition here is that the ionization must attain the density N for
the appearance of the discharge. The critical point occurs at he intersection
of these two controlling conditions.
The constants, V and d in equations 6 and 7, are easily determined. The method of finding V has been previously explained. The constant d is the intersection of the asymptote to the curve with the axi of coordinates.
The mean free path of an ion at a given pressure may be obtained by solving equation (6) for two values of X corresponding to the two value of T. The two equations so obtained also give the value of a, which is a constant for all pressures and frequencies. The results obtained for the three gases are given in the following table:
| v | d |  / / | a | p | |
|---|---|---|---|---|---|
| Air | 4.4 | 1 | 4.4 | 28.5 | 2.4 |
| CO2 | 7.6 | 2.5 | 4.3 | 31.5 | 1.8 |
| Helium | 8 | 3.8 | 3.4 | 33 | 1.66 |
V and d are constants previously explained.  /
/ is the ratio of
the mean free path of an ion to that of a molecule. The constant a
is the number of successive impacts which the N0
ions make during the time of a half oscillation. P is the number
of volts through which an ion must run to produce ions by collision.
is the ratio of
the mean free path of an ion to that of a molecule. The constant a
is the number of successive impacts which the N0
ions make during the time of a half oscillation. P is the number
of volts through which an ion must run to produce ions by collision.
The ionization is due to the impact of negative ions only. The positive ions, owing to their greater mass, run through only a small part of their mean free path in the time T, while on the other hand the negative ions make a successive impacts in the same time.
My thanks are due to Professor J. J. Thomson for his cordial advice and interest during the progress of this work at the Cavendish Laboratories. I wish also to acknowledge my obligations to the John Tyndall fellowship fund of Columbia University which made this work at the Cavendish Laboratorie possible.
Figure 1
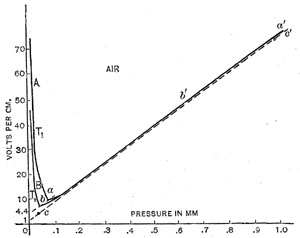
Figure 2
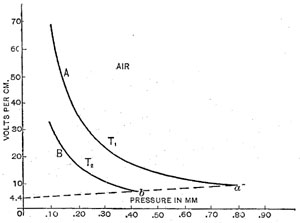
This is the part of the curves from Figure 1 for pressures below the minimum shown on an enlarged scale
Figure 2

This is the part of the curves from Figure 1 for pressures below the minimum shown on an enlarged scale