G. Hanson, G. S. Abrams, A. M. Boyarski, M. Breidenbach, F. Bulos, W. Chinowsky, G. J. Feldman, C. E. Friedberg, D. Fryberger, G. Goldhaber, D. L. Hartill, B. Jean-Marie, J. A. Kadyh, R. R. Larsen, A. M. Litke, D. Lüke, B. A. Lulu, V. Lüth, H. L. Lynch, C. C. Morehouse, J. M. Paterson, M. L. Perl, F. M. Pierre, T. P. Pun, P. A. Rapidis, B. Richter, B. Sadoulet, R. F. Schwitters, W. Tanenbaum, G. H. Trilling, F. Vannucci, J. S. Whitaker, F. C. Winkelmann, and J. E. Wis

Lawrence Berkeley Laboratory and Department of Physics, University of California, Berkeley, California 94720, and Stanford Linear Accelerator Center, Stanford University, Stanford, California 94305

(Received 8 October 1975)

We have found evidence for jet structure in e⁺e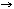^-hadrons at center-of-mass energies of 6.2 and 7.4 GeV. At 7.4 GeV the jet-axis angular distribution integrated over azimuthal angle was determined to be proportional to 1 + (0.78 ± 0.12) cos² .

In quark-parton constituent models of elementary particles, hadron production in e⁺e^- annihilation reactions proceeds through the annihilation of the e⁺ and e^- into a virtual photon which subsequently produces a quark-parton pair, each member of which decays into hadrons. At sufficiently high energy the limited transverse-momentum distribution of the hadrons with respect to the original parton production direction, characteristic of all strong interactions, results in oppositely directed jets of hadrons.^1-4 The spins of the constituents can, in principle, be determined from the angular distribution of the jets.

In this Letter we report the evidence for the existence of jets and the angular distribution of the jet axis.

The data were taken with the Stanford Linear Accelerator Center-Lawrence Berkeley Laboratory magnetic detector at the SPEAR storage ring of the Stanford Linear Accelerator Center. Hadron production, muon pair production, and Bhabha scattering data were recorded simultaneously. The detector and the selection of events have been described previously.^5,6 The detector subtended 0.65 x 4 ¼ sr with full acceptance in azimuthal angle and acceptance in polar angle from 50° to 130°. We have used the large blocks of data at center-of-mass energies (E_c.m.) of 3.0, 3.8, 4.8, 6.2, and 7.4 GeV. We included only those hadronic events in which three or more particles were detected in order to avoid background contamination in events with only two charged tracks due to beam-gas interactions and photon-photon processes.

To search for jets we find for each event that direction which minimizes the sum of squares of transverse momenta.⁷ For each event we calculate the tensor

(1)

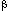where the summation is over all detected particles and and refer to the three spatial components of each particle momentum 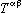. We diagonalize 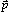to obtain the eigenvalues ₁, ₂, and ₃ which are the sums of squares of transverse momenta with respect to the three eigenvector directions. The smallest eigenvalue (₃) is the minimum sum of squares of transverse momenta. The eigenvector associated with ₃ is defined to be the reconstructed jet axis. In order to determine how jetlike an event is, we calculate a quantity which we call the sphericity (S):

(2)

S approaches 0 for events with bounded transverse momenta and approaches 1 for events with large multiplicity and isotropic phase-space particle distributions.

The data at each energy were compared to Monte Carlo simulations which were based on either an isotropic phase-space (PS) model or a jet model. In both models only pions (charged and neutral) were produced. The total multiplicity was given by a Poisson distribution. The jet model modified phase space according to the square of a matrix element of the form

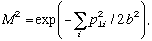
(3)

where 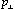is the momentum perpendicular to the jet axis.

The angular distribution for the jet axis is expected to have the form

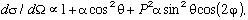
(4)

where is the polar angle of the jet axis with respect to the incident positron direction, is the azimuthal angle with respect to the plane of the storage ring, = (_T - _L)/(_T + _L) with _T and _L the transverse and longitudinal production cross sections, and P is the polarization of each beam. (The polarization termwill be discussed later.) The angular distribution given by Eq. (4) was used in the jet-model simulation. The simulations included the geometric acceptance, the trig ger efficiency, and all other known characteristics of the detector. The total multiplicity and the charged-neutral multiplicity ratio for both models were obtained by fitting to the observed charged-particle mean multiplicity and mean momentum at each energy. In the jet model the parameter b was determined by fitting to the observed mean S at the highest energy (7.4 GeV). For lower energies the value of b was determined by requiring that the mean 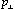in the jet model be the same (315 MeV/c) as at 7.4 GeV.

Figure 1: Observed mean sphericity versus center-of-mass energy Ec.m. for data, jet model with <> = 315 MeV/c (solid curve), and phase-space model (dashed curve).

Figure 2: Observed sphericity distributions for data, jet model with <> = 315 MeV/c (solid curves), and phase-space model (dashed curves) for (a) Ec.m.=3.0 GeV; (b) Ec.m.=6.2 GeV; (c) Ec.m.=7.4 GeV; and (d) Ec.m.=7.4 GeV, events with largest x<0.4. The distributions for the Monte Carlo models are normalized to the number of events in the data.

Figure 1 shows the observed mean S and the model predictions. Both models are consistent with the data in the 3-4-GeV region. At higher energies the data have significantly lower mean S than the PS model and agree with the jet model. Figure 2 shows the S distributions at several energies. At 3.0 GeV the data agree with either the PS or the jet model [Fig. 2(a)]. At 6.2 and 7.4 GeV the data are peaked toward low S. favoring the jet model [Figs. 2(b) and 2(c)]. At the highest two energies, the PS model poorly reproduces the single-particle momentum spectra, having fewer particles with x > 0.4 (x=2p/E_c.m. and p is the particle momentum) than the data.⁸ The jetmodel x distributions are in better agreement. For x < 0.4 the x distributions for both models agree with the data. Therefore, we show in Fig. 2(d) the S distributions at 7.4 GeV for those events in which no particle has x > 0.4. The jet model is still preferred.

Figure 3: Observed distributions of jet-axis azimuthal angles from the plane of the storage ring for jet axes with |cos|¾0.6 for (a) Ec.m.=6.2 GeV and (b) Ec.m.=7.4 GeV.

Figure 4: Observed inclusive versus x (from Ref. 9) for particles with |cos |¾0.6 in hadronic events at Ec.m.=7.4 GeV. The prediction of the jet-model Monte Carlo simulation for jet-axis angular distribution with =0.78±0.12 is represented by the shaded band.

At E_c.m. = 7.4 GeV the electron and positron beams in the SPEAR ring are transversely polarized, and the hadron inclusive distributions show an azimuthal asymmetry.⁹ The distributions of the jet axis for jet axes with |cos | ¾ 0.6 are shown in Fig. 3 for 6.2 and 7.4 GeV.¹⁰ At 6.2 GeV, the beams are unpolarized⁹ and the distribution is flat, as expected. At 7.4 GeV, the distribution of the jet axis shows an asymmetry with maxima and minima at the same values of as for e⁺e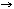^- µ⁺µ^-.

The distribution shown in Fig. 3(b) and the value for P² (0.47 ± 0.05) measured simultaneously by the reaction⁹ e⁺e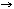^- µ⁺µ^- were used to determine the parameter of Eq. (4). The value obtained for the observed jet axis is = 0.45 ± 0.07. This observed value of will be less than the true value which describes the production of the jets because of the incomplete acceptance of the detector, the loss of neutral particles, and our method of reconstructing the jet axis. We have used the jet-model Monte Carlo simulation to estimate the ratio of observed to produced values of and find this ratio to be 0.58 at 74 GeV. Thus the value of describing the produced jet -axis angular distribution is = 0.78 ± 0.12 E_c.m. = 7.4 GeV. The error in is statistical only; we estimate that the systematic errors in the observed can be neglected. However, we have not studied the model dependence of the correction factor relating observed to produced values of .

The sphericity and the value of as determined above are properties of whole events. The simple jet model used for the sphericity analysis can also be used to predict the single-particle inclusive angular distributions for all values of the secondary particle momentum. In Fig. 4 values for the inclusive hadron as a function of x at 7.4 GeV⁹ are compared with the jet-model calculation. The model assumed the value = 0.78 ± 0.12 for the jet-axis angular distribution. The prediction agrees well with the data for all values of x.

We conclude that the data strongly support the jet hypothesis for hadron production in e⁺e^- annihilation. The data show a decreasing mean sphericity with increasing E_c.m. and the sphericity distributions peak more strongly at low values as E_c.m. increases. Both of these trends agree with a jet model and disagree with an isotropic PS model. The mean transverse momentum relative to the jet axis obtained using the jet-model Monte Carlo simulation was found to be 315 ± 2 MeV/c. At E_c.m. = 7.4 GeV the coefficient for the jet-axis angular distribution in Eq. (4) has been found to be nearly + 1 giving a value for _L/_T of 0.13 ± O.07. The jet model also reproduces well the inclusive hadron versus x. All of this indicates not only that there are jets but also that the helicity along the jet axis is ± 1. In the framework of the quark-parton model, the partons must must have spin 1/2 rather than spin 0.

1. S. D. Drell, D. J. Levy, and T. M. Yan, Phys. Rev. 187, 2159 (1969), and Phys. Rev. D 1, 1617 (1970).
2. N. Cabibbo, G. Parisi, and M. Testa, Lett. Nuovo Cimento 4, 35 (1970).
3. J. D. Bjorken and S. J. Brodsky, Phys. Rev. D 1, 1416 (1970).
4. R. P. Feymann, Photon-Hadron Interactions (Benjamin, Reading, Mass., 1972), p. 166.
5. J.-E. Augustin et al., Phys. Rev. Lett. 34, 233 (1975) .
6. J.-E. Augustin et al., Phys. Rev. Lett. 34, 764 (1975) .
7. It is impossible to determine the jet axis exactly, even with perfect detection efficiency; the method described here, which was suggested in Ref. 3, is the best approximation known to us.
8. The momentum distributions will be discussed in a subsequent paper.
9. R. E. Schwitters et al., Phys. Rev. Lett. 35, 1320 (1975) .
10. Since the jet axis is a symmetry axis, the azimuthal angle + 180° is equivalent to the azimuthal angle .