SOME PHYSICS HISTORY

Crystal Statistics II
Partition Function Evaluated by Spinor Analysis

Bruria Kaufman
Columbia University, New York City, New York

(Received May 11, 1949)

The partition function for a 2-dimensional binary alloy has been evaluated exactly by Onsager, using the approach introduced by Kramers and Wannier, and Montrol. According to this method, a matrix characteristic of the crystal is set up, and it is shown that the partition function is approximately equal to the largest eigenvalue of the characteristic matrix. The eigenvalue problem has been treated approximately by various authors. Onsager has shown that the characteristic matrix is decomposable into a direct product of 2-dimensional matrices and so was able to find the exact eigenvalues through the solution of n-quadratic equations.

In this paper, a shorter method, though closely related, is employed to reduce the characteristic matrix, V. It is shown that V is a 2ⁿ-dimensional "spin"-representative of a 2n-dimensional rotation (i.e., orthogonal matrix), and that, as a consequence, its eigenvalues were known as soon as the eigenvalues of the rotation were given. Further considerations of symmetry reduce the 2n-dimensional matrix into a product of n-plane rotations, so that again the eigenvalues are found from the solution of n-quadratic equations.

As a by-product of the solution of the eigenvalue problem, we are also able to find the matrix 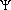of eigenvectors of V. Since every operation in 2ⁿ-space is mirrored in the 2n-dimensional space, the operation of 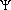corresponds to the digonalization of the 2n-dimensional rotation. This latter operation is easy to carry out, again because of the symmetry of the 2n-dimensional rotation.

As has been shown, the knowledge of 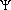makes it possible to state the average probabilities of crystal configurations. In particular, it is possible to evaluate average correlations between pairs of atoms within the crystal. This will be done in III.

1. Setting Up the Matrix Problem

Our physical model is a rectangular lattice with m rows and n sites per row. These sites are to be occupied by two kinds of constituent atoms. We assume that interactions exist only between nearest neighbors, and that the energy of interaction is +J between unlike neighbors in a row, or column, respectively. The total energy of a configuration of the lattice is found simply by counting the number of like neighbors in the lattice, and subtracting from it the number of unlike neighbors. (Since we must distinguish between row and column interactions, this count has to be made separately for the J and the J' (see Fig. 1).)

The probability of finding the lattice in a given configuration, at the temperature T, is proportional to exp{-E_c/kT}, where E_c is the total energy of the configuration. Clearly, the exponent which appears in the expression for the probability will always be of the form

Here n_c, n_c' are integers which depend on the configuration of the lattice. It is convenient to introduct the variables H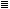J/kT, H'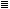J'/kT instead of J, J'. And then the probability of a configuration i

Z is the "partition function" for the lattice,

The thermodynamic functions for the crystal can be found from a knowledge of Z, and, as can be seen from its definition, it is a simple matter to calculate Z for small crystals. However, since the number of terms in Z is 2^m·n, it is not feasible to carry out such a calculation except when m and n are of the order of unity. Nor is it necessary to proceed in such a tedious manner. It has been shown that the terms in Z are members of the mth power of a matrix V which is characteristic for the lattice. Z is then seen to be the trace of V^m.

To show this, it is convenient to introduct the fiction of spin attributed to each atom. All atoms of one kind will be given the spin +1, and the other kind -1. When this is done, the interaction between two neighboring atoms with spins 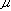, 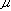' is: -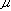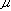'H (or -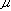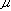'H') for row (or column) neighbors.

The configurations of the crystal can now be specified by stating the value of 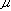at each site of the crystal. However, it is more convenient to specify row-configurations. Since there are n atoms in a row, there are 2ⁿ possible configurations, 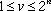. And then the configuration of the crystal is given by the set {v₁, v₂,...,v_m}.

The energy due to interactions within a row may be denoted by E(v_i); the energy due to interaction between two adjacent rows-by E(v_i,v_i+1). As a result, the energy of a configuration of the crystal i

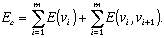
(Here it is assumed, for purposes of symmetry, that the mth row of the crystal interacts with the first row.) If we now make the abbreviation

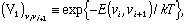(1)

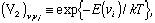(2)

we see that the probability of a configuration is proportional to

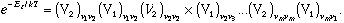
We therefore get for the partition function

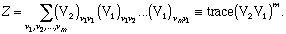(3)

Since for each i: 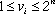, we see that V₁ and V₂ are 2ⁿ-dimensional matrices, and V₂ is diagonal. V₁ and V₂ have been given explicitly in I:

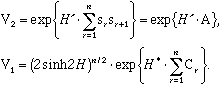(4)

Here s_r and C_r are 2ⁿ-dimensional quarternion matrices,

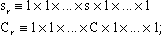(5)

there are n factors in each direct-product, with s or C appearing in the rth position. s and C are generators of the Pauli matrices:

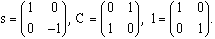(6)

H^* is defined by

(7)

We may redefine V₁ so as to remove from it the scalar coefficient:

(8)

Then

(9)

where _i are the eigenvalues of VV₂·V₁.

We now propose to show that matrices of the type exp(a·s_rs_r+1), exp{b·C_r}, and their products, form a 2ⁿ-dimensional representation of the group of rotations in 2n-dimensions. Thus, the matrix V itself will be the representative of some such rotation.

We will further show that there is a very simple relationship between the eigenvalues of the rotation and the eigenvalues of its 2ⁿ-dimensional representative. As a result, all our work will be reduced to finding eugenvalues in a 2n-dimensional space.

Full text is available from The Physical Review Second Series, October 15, 1949, vol. 76 no. 8, pp. 1232-1243.

[Back]