SOME PHYSICS HISTORY

Crystal Statistics III
Short-Range Order in a Binary Ising Lattice

Bruria Kaufman
The Institute for Advanced Study, Princeton, New Jersey

Lars Onsager
Yale University, New Haven, Connecticut

(Received May 11, 1949)

1. Definition of the Degree of Order

The "degree of order" in a crystal composed of several kinds of atoms is an observable, as is shown by x-ray diffraction studies. Several attempts have been made to interpret the degree of order quantitatively, so that a functional dependence of order upon temperature could be stated. In this paper we use a statistical approach to find the average, taken over all configurations of the crystal, of the correlation between a pair of atoms within the crystal. This correlation will be a function of the temperature, and will depend on the relative position of the atoms in the pair. Since only relative positions enter here, we may keep one of the atoms fixed and consider the family of correlation curves for all pairs in which our fixed atom is a member. This family of curves will describe the degree of order within the crystal.

In order to define, and evaluate, the correlation functions in a formal way, we must rely upon the results of previous papers, I and II; we will make use of the spinor-analysis method introduced in II.

The model we use is, as in the previous papers, a two-dimensional rectangular lattice, with a spin variable 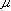=±1 at each lattice site. It is assumed that only nearest neighbors interact, and that at zero temperature the perfectly ordered crystal has all its spins aligned in one direction (either 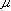=+1 for all lattice sites, or 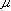=-1 for all sites). It has been shown that all the information about probabilities of configurations could be presented in a compact way with the help of a matrix V having 2ⁿ rows and columns, such that for example the partition function for the lattice become

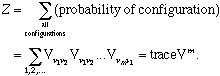(II. 3)

Here v_i is the configuration of the ith row, that is to say, the specification of the values of 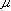for all the n atoms in this row ( 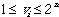for all ).

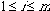Using the matrix V, we can also write the average values of various functions of the configurations of the lattice. Such functions must be weighted in each configuration by the probability of the configuration, and so we find that the average of the function 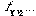i

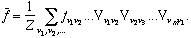(1)

The Correlation Functions

The spin of the jth site in any given row (say row k) is clearly a function of the configuration of the lattice. It depends only on the configuration of its own row, i.e., on v_k. And it is easy to see that as v_k goes through its range of values (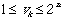), the spin under consideration takes on the values +1 or -1 in a particular order, which is the order of the diagonal elements in the (diagonal) matrix 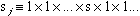(n factors). (The notation is as in I:

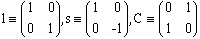
are the Pauli matrices; stands for direct product of matrices). As an example, consider the simple case n=2. v_k has 2²=4 possibilities: + +, + -, - +, - -. Correspondingly, the spin of the left-hand site is: +1, +1, -1, -1. But these are the diagonal elements (in that order) of s1. The spin of the right-hand site is: +1, -1, +1, -1, which can be read off the diagonal of the matrix 1s. In general the spin of the jth site in the kth row, when the crystal is in configuration {v₁, v₂,..., v_m}, is .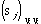

We can now find the average value of this spin:

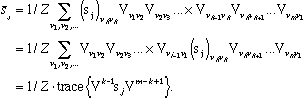(2)

Since the trace is invariant with respect to cyclic changes in the order of factors we have

(3)

This result is independent of k, as it should be. It will be seen later that vanishes identically for every j, and this is not surprising because a priorievery site has the same probability of being occupied by a positive spin as by a negative one, at all temperatures.

The situation is different for the correlation between two sites. Consider the product of the spins of site k in row j and site b in row a. The average of this product will be:

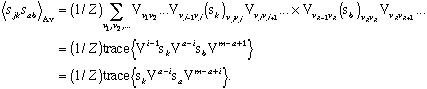(4)

This average value will not vanish. At zero temperature, all spins are aligned, so that 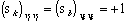and therefore 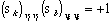. As a result

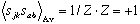
for all pairs of sites. This is the state of perfect order. At higher temperatures 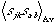decreases, and tends to zero for very high T.

We will refer to 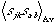as the correlation between the two sites (j,k) and (a,b), and will take the set of all these functions to be a measure of the degree of order within the crystal. Short-range order is described by the correlations for finite (small) distances beteween the sites. Long-range order is the limit for great distances, and will be discussed in Part IV.

In what follows, we will show how to evaluate the correlations as functions of temperature for successive distances between pairs of sites. Part of the work in the evaluation of these averages is algebraic: it is necessary to find the trace of the appropriate matrices, as given in (4). This will be simple for a-j=0,1. For larger distances between rows the procedure, while still straightforward, is quite tedious. The algebraic work will give the correlation in terms of sums of the form

These sums are then evaluated (with the help of a elliptic substitution) for the case of a quadratic crystal: H=H'. A particularly simple result obtains at the critical temperature, where . The value of 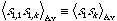can then be computed to any desired distance. It is found that

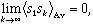
but this limit is approached very slowly.

Full text is available from The Physical Review Second Series, October 15, 1949, vol. 76 no. 8, pp. 1244-1252.

[Back]