E. Noether's Discovery of the Deep Connection Between Symmetries and Conservation Laws
Nina Byer
Physics Department
University of California at Los Angeles
Los Angeles, CA. 90095
Abstract
Emmy Noether's paper "Invariante Varlationsprobleme" [1], hereafter referred to as I.V., profoundly influenced 20th century physics. It was presented to the July 16, 1918 meeting of the Könighche Gesellschaft der Wissenschaften zu Göttingen by Felix Klein presumably because Noether was not a member of the Gesellschaft1. One wonders if she was even present when the paper was read. The paper proved two theorems and their converses which revealed the general connection between symmetries and conservation laws in physics. They led to a deeper understanding of laws such as the principles of conservation of energy, angular momentum, etc., and also were instrumental in the great discoveries of gauge field symmetries of the 20th century. [2]
Remarkably these theorems are something of a departure from the main line of Noether's mathematical research, which was the development of modern abstract algebra. An examination of the historical circumstances in which she made these discoveries sheds light on how she came to do this work. The work followed upon David Hilbert's discovery of the variational principle from which he derived the field equations of general relativity. At this time David Hilbert, Felix Klein and others in Göttingen were intensely interested in the recently completed general theory of relativity. There were unresolved issues regarding the question of energy conservation in the theory. Published correspondence [3] between Hilbert and Klein regarding this indicates that Noether's help was requested by Hilbert to clarify these issues, and that she then did the work whose results are published a few years later in I.V.. The discussion and proofs of the two theorems in I.V. clarified and resolved the issues regarding energy conservation, as Hilbert acknowledged in his 1924 Grundlagen der Physik article [4]. From her Collected Works [5], it would seem that after this and some additional work on differential invariants in general relativity [6], Noether returned to the main line of her mathematical research.
Here I will present first a chronology of events leading up to Noether' publication of the I.V. paper; then a discussion of some rather difficult issues regarding energy conservation in general relativity which her work resolved; and finally a description and discussion of the two theorems in the I.V. paper.
In 1915, Emmy Noether was invited to join the team of mathematicians assembled in Göttingen by David Hilbert. Hermann Weyl reports [7]: "To both Hilbert and Klein, Emmy was welcome as she was able to help them with invariant-theoretic knowledge." She was thirty-three at that time, having received a doctorate in mathematics from the University of Erlangen seven year earlier, and written the eleven papers listed in Appendix A. The first in the list is her thesis which was done under the supervision of Paul Gordan. For her thesis she calculated all the 331 invariants of ternary bi-quadratic forms! Shortly thereafter she took the abstract approach to algebra following Hilbert' 1888 basis theory paper. She worked unpaid in Erlangen supervising students and sometimes lecturing for her ailing father. After her father died, she joined Hilbert and his team in Göttingen. [8]
In June-July 1915, shortly after Noether arrived, Albert Einstein gave six lectures in Gottingen on the general theory of relativity. At that time the theory was not yet finished; he had not yet found the complete field equations. However, the basic ideas were clear and his audience found them compelling. After giving the lectures, Einstein said [9]: "To my great joy, I completely succeeded in convincing Hilbert and Klein." He had been working to generalize the special theory of relativity to include gravity since 1905. In 1907 he discovered the importance of the equality of gravitational and inertial mass and formulated the equivalence principle, but it took another eight years to complete the theory. Finally in November 1915, having found the complete field equation, he submitted the famous paper [10] that gives the theory in its final form. Remarkably, in the same month, Hilbert submitted a manuscript [11] in which the same field equations are obtained as the solution to a variational problem. Hilbert and Einstein had independently found the field equations at about the same time [9]. In November 1915, Emmy Noether wrote to Ernst Fischer: "Hilbert plans to lecture next week about his ideas on Einstein' differential invariants,and so .. [we] had better be ready" [8]. It would seem, therefore, that she began to study relativity theory then. Out of that study came two papers which Hermann Weyl characterized as giving "the genuine and universal mathematical formulation of two of the most significant aspects of general relativity theory: first, the reduction of the problem of differential invariants to a purely algebraic one by use of normal coordinates; and second, the identities between the left sides of Euler' equations of a problem of variation ..." [7]. Regarding the first paper referred to by Weyl [6], Einstein wrote to Hilbert: "Yesterday I received from Miss Noether a very interesting paper on invariant forms. I am impressed that one can comprehend thesematters from so general a viewpoint. It would not have done the old guard at Göttingen any harm had they picked up a thing or two from her. ..." [12]. The second paper referred to by Weyl is the I.V. paper we will discuss at length.
Hilbert had been interested in the fundamental laws of physics for many years [13]. The paper in which he published his derivation of the field equations for general relativity is entitled Grundlagen der Physik [11]. It was an early effort to formulate a unified field theory of gravity, electromagnetism, and matter. In this was unsuccessful, and Hilbert omitted this paper from his collected work [14]. However, when specialized to gravity, Hilbert' derivation of the field equations is an original and important contribution to the general theory. The Lagrangian he introduced is known as the Hilbert-Einstein Lagrangian, and his formulation of the theory is in widespread use today. Pais writes: "Hilbert was not the first to apply the principle to gravitation. Lorentz had done so before him. So had Einstein, a few week earlier. Hilbert was the first, however, to state this principle correctly." As regards Hilbert's 1915 paper, Hermann Weyl [13] wrote: "Einstein's more sober procedure ... [has] proved the more fertile. Hilbert' endeavors must be looked upon as a forerunner of a unified field theory of gravitation and electromagnetism. However, there was still much too much arbitrariness involved in Hilbert's Hamiltonian function; subsequent attempt (by Weyl, Eddington, Einstein himself, and others) aimed to reduce it. .. But the problem of a unified field theory stands to this day as an unsolved problem."
Though the general theory of relativity was completed in 1915, there remained unresolved problems. In particular, the principle of local energy conservation was a vexing issue. In the general theory, energy is not conserved locally as it is in classical field theories - Newtonian gravity, electromagnetism, hydrodynamics, etc.. Energy conservation in the general theory has been perplexing many people for decades. In the early days, Hilbert wrote about this problem as 'the failure of the energy theorem '. In a correspondence with Klein [3], he asserted that this 'failure' is a characteristic feature of the general theory, and that instead of 'proper energy theorems' one had 'improper energy theorems' in such a theory. Thi conjecture was clarified, quantified and proved correct by Emmy Noether. In the note to Klein he reports that had requested that Emmy Noether help clarify the matter. In the next section this problem will be described in more detail and an explanation given of how Noether clarified, quantified, and proved Hilbert' assertion. One might say it is a lemma of her Theorem II.
Klein was working on this problem of energy conservation, or as he termed it Hilbert's energy vector, in 1916. He wrote in thi correspondence with Hilbert that "Frl. Noether advised me continually throughout my work, and it was really only through her that I was led to the material presented in this letter. When I spoke recently with Frl. Noether about my result concerning your energy vector, she told me that she had derived the same thing from your Note2 a year ago and written it up in a manuscript (which I examined). " Klein presented a paper with his results on Hilbert's energy vector to the July 19 meeting of the Gesellschaft. In this paper [14], he acknowledges helpful contributions from Noether. However, in the annotation to this paper hi collected works he makes it clear that his result is a special case of her 'far-reaching' theorem. He reports that he presented her paper to the Gesellschaft the following week, and says that she also proved and generalized some of Hilbert's ideas. An English translation of that interesting annotation is given in Appendix B.
In his famous 1924 Grundlagen der Physik paper3, David Hilbert credits Emmy Noether with having solved the problem of an energy theorem in the general theory, and refers to I.V.. In the concluding section of her paper, she refers to Hilbert' having said that 'the failure of the energy theorem' is a characteristic feature of the general theory. The last section is entitled "A HILBERTIAN ASSERTION", and says in part [16]: "From the foregoing ... [we] obtain the proof of an assertion of Hilbert concerning the connection between the failure of proper energy conservation laws and general relativity, and indeed in a general group- theoretic setting." It seems to me this remark is a notable understatement. Her powerful results are deep and general; far more than simply a verification of Hilbert's assertion.
In 1919, Noether chose I.V. for her Habilitation thesis and presented it to the University of Gttingen along with the twelve previously published papers and two additional manuscripts, one of which [17] contained a number of important ideas which had a significant impact on the development of modern abstract algebra. Years before she had been refused Habilitation the right to lecture under University auspices). Hermann Weyl records [17] "during the war Hilbert tried to push through Emmy Noether's Habilitation in the Philosophical Faculty in Gttingen. He failed due to the resistance of the philologists and historians. It is a well-known anecdote that Hilbert .[declared] at the faculty meeting; 'I do not see that the sexof a candidate is an argument against her admission as Privatdocent. After all, we are a university not a bathing establishment.' "It was only after the liberalization of Germany in the post-WWI period that Habilitation was granted, and she was finally able to lecture officially at the University. She had given lectures in the preceeding years, but the posted notices stated that they were offered by Herr Professor David Hilbert, given by Frl. E.Noether, with no tuition required. These lectures were becoming famous and drawing the attendance of mathematicians from all over Europe. Without Habilitation she was working unpaid.
It is quite clear from the application papers written for Habilitation that Noether knew the scope and importance of her results for physics. She wrote about the I.V. paper [8]"... The general results contain, as special cases, theorems on first integral [conservation laws] ... in mechanics; furthermore, conservation theorems and interdependences among the field equations in the theory of relativity... " She remarks that this work was "an outgrowth of my assistance to Klein and Hilbert in their work on Einstein's general theory of relativity."
In contemporary terminology the general theory of relativity is a gauge theory. The symmetry group of the theory, is a gauge group. It i the group of all continuous coordinate transformations with continuou derivatives, often called the group of general coordinate transformations. It is a Lie group that has a continuously infinite number of independent infinitesimal generators. In Noether's terminology such a group is an infinite continuous group. The symmetry group of special relativity, the Poincare' group4 is a Lie subgroup of the group of general coordinate transformations. It has a finite number (7) of independent infinitesimal generators. Noether refers to such a group as a finite continuou group. This distinction between a Lie group with a finite (or countably infinite) number of independent infinitesimal generators and an infinite continuous group is what distinguishes Noether's theorem I and theorem II in I.V.. Theorem I applies when one has a finite continuous group of symmetries, and theorem II when there is an infinite continuous group of symmetries. Field theories with a finite continuous symmetry group have what Hilbert called `proper energy theorems'. Physically in such theories one has a localized, conserved energy density; and one can prove that in any arbitrary volume the net outflow of energy across the boundary is equal to the time rate of decrease of energy within the volume. As will be shown below, this follow from the fact that the energy-momentum tensor of the theory is divergence free. In general relativity, on the other hand, it has no meaning to speak of a definite localization of energy. One may define a quantity which is divergence free analogous to the energy-momentum density tensor of special relativity, but it is gauge dependent: i.e., it is not covariant under general coordinate transformations. Consequently the fact that it is divergence free does not yield a meaningful law of local energy conservation. Thus one has, as Hilbert saw it, in such theories `improper energy theorems.'
A key feature for physics of Noether's I.V. paper is the clarity her theorems brought to our understanding of the principle of energy conservation. As Feza Gursey wrote [18]: "Before Noether' Theorem the principle of conservation of energy was shrouded in mystery, leading to the obscure physical systems of Mach and Ostwald. Noether's simple and profound mathematical formulation did much to demystify physics." Noether showed in her theorem I that the principle of energy conservation follows from symmetry under time translations. This applies to theories having a finite continuous symmetry group; theories that are Galilean or Poincar invariant, for example. In general relativity, on the other hand, energy conservation takes a different form as will be shown below. Noether's theorem 11 applies in the case of general relativity and one sees that she has proved Hilbert's assertion that in this case one has `improper energy theorems', and that this is a characteristic feature of the theory. It is owing to the fact that the theory is a gauge theory; i.e., that it has an infinite continuous group of symmetrie of which time translations are a subgroup. Indeed generally she defines a `improper' divergence relationships, which vanish when the field equations are satisfied, which correspond to a finite continuous subgroup of an infinite continuous group. Generally they do not have the required invariance or covariance properties under the larger group. For example, in general relativity a divergence free energy-momentum (pseudo) tensor can be constructed but it is gauge dependent (see below). Because it is not covariant under general coordinate transformations, it is more properly called a pseudotensor. Such pseudotensors are covariant with respect to the linear transformations of the Poincar group and may be used in asymptotic spacetime regions far from gravitating sources to derive a principle of energy conservation. [19]
To illucidate these matters further, we discuss in some detail field theories of matter, gravity, electromagnetism, etc. in both special and general relativity. In special relativity these theories have a `proper energy theorem' in the sense of Hilbert and we will show how `proper energy theorems' give a principle of local energy conservation. In general relativity, on the other hand, the proper energy theorem becomes improper in that the energy-momentum tensor for which the theorem holds is gauge dependent. As will be shown below, there is transfer of energy to and from the gravitational field and it has not meaning to speak of a definite localization of the energy of the gravitational field in space5. Consequently we do not have a principle of local energy conservation in spacetime regions in which there exist gravitational fields.
The theories we discuss here are field theories which may be formulated in terms of a variational principle; i.e., their field equations may be obtained from Hamilton's principle. This was Hilbert's great contribution to the general theory of relativity. He showed the correct field equations can be derived from Hamilton's principle, and Noether's work followed upon this. In this formulation, the theory is defined by a Lagrangian L. The field equation are derived from Hamilton's principle that the action
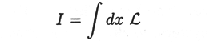 | (1) |
is an extremum. The Lagrangian depends on the field quantities and their derivatives. Symbolically let phi represent the field quantities and, for simplicity, assume L depends only on phi and its first derivatives. Then Hamilton's Principle gives the field equations: viz.,
|
| (2) |
Here we discuss in some detail laws of energy conservation in special and general relativity where Noether's theorem I applies in the first case and theorem II in the second.6 When the action is invariant with respect to transformations of the Poincar group, Noether' theorem I gives a divergence-free energy-momentum tensor T mu nu(x) which, symbolically in the notation of (2), for scalar fields is given by 7
|
| (3) |
More generally one may write the energy-momentum tensor as 8
|
| (4) |
Theorem I shows invariance of the action under spacetime translations implies that the divergence of T mu nu is proportional to the left side of (2) 9. Consequently when the field equations are satified, the divergence vanishes and we have 10
|
| (5) |
This implies local energy conservation. The energy density
at the spacetime point x is given by the T00(x)
and the T0i(x) components give the energy crossing a
unit area per unit time in the direction of the normal i. The time-like
equation (5), i.e., with mu = 0, follows from the invariance of the theory
under time translations. To show that
this gives local energy conservation, it is convenient to use a 3-vector F
for
the T0i components; then (5) read
|
| (6) |
Integration of (6) over any spatial volume V shows, by Gauss's theorem, that the rate of change of energy in V equals the net energy flow across the bounding surface per unit time. This holds for arbitrary and, therefore, arbitrarily small volumes. Thus (5) gives, in the language of contemporary physicists, local energy conservation. This is a `proper energy theorem' in the sense of Hilbert.
In general relativity, on the other hand, the components of the metric tensor gmu nu are the gravitational field variables and generally spacetime dependent. They are included as field variables in the Lagrangian of the theory with the addition of the Hilbert-Einstein term R; L has in it, as before, the electromagnetic, matter, etc. field variables. The action i
|
| (7) |
where g is the determinant of g mu nu is a coupling constant and R is the Riemannian curvature scalar. Following Hilbert, one may derive the field equations of general relativity from the condition that (7) is an extremum with respect to variations of g mu nu . One obtain
|
| (8) |
where Rmu nu is the Ricci tensor constructed by contraction from the Riemann curvature tensor, and R is the Ricci or curvature scalar. The Riemann curvature tensor is constructed from the metric tensor g mu nu and its first and second derivatives. The source term on the right side of (8) is the energy-momentum tensor Tmu nu given by (4).[19] It contains contributions from the electromagnetic fields, matter fields, etc. but not from gravitational fields. Since gravitational fields carry energy and momentum, T00 is not the total energy density. As will be shown below, Tmu nu is not divergence-free. It cannot and does not play the same role as regard energy-momentum conservation as in special relativity. This surely wa immediately clear to Hilbert in 1915. What was apparently not clear to Hilbert and Klein in the early days was how the principle of conservation of energy i satisfied in this theory. This will be discussed below.
For theories whose symmetry group is an infinite continuou group, the main results of theorem II are that there are certain identities, or "dependencies" as she called them [1], between Lagrange functions of the theory and their derivatives. This is quite different from the results of theorem I that for each infinitesimal generator of the finite continuous group there is a quantity whose divergence vanishes when the Lagrange functions vanish (field equations are satisfied). In general relativity, the "dependencies" give the Bianchi identities for components of the curvature tensor. These results are covariant under the full group. In particular, one has the contracted Bianchi identity
|
| (9) |
This equation states that the covariant divergence of the left side of (8) vanishes. The covariant divergence differs substantially from the ordinary divergence which we have been discussing up to now. For a second rank tensor, e.g. Tmu nu , the covariant divergence is given by
|
| (10) |
where the Christoffel symbols (the gamma symbols) depend upon the metric tensor gmu nu and it derivatives and are non-vanishing when the Riemann curvature is different from zero. The covariant divergence is an invariant; i.e., the covariant divergence of a second rank tensor gives a first rank tensor. Thus (9) implie
|
| (11) |
This is often referred to as the energy-momentum conservation law for general relativity. The presence of the metric tensor and it derivatives in (10) shows the energy-momentum transfer contained in (11) between the gravitational fields and the source fields in T mu nu .
From (10) it is clear the ordinary divergence T mu nu, nu is in general different from zero in spacetime regions with gravitational fields. It is interesting to note, however, that at any given spacetime point one may choose a set of coordinates for which the gravitational fields vanish (gmu nu reduces to the flat spacetime Minkowski metric and the Christoffel symbols vanish). This is guaranteed by the equivalence principle which states that one can always choose a coordinate system such that spacetime in the neighborhood of a given point is Minkowski (flat). Thus one may see why it is not meaningful to speak of a localized energy density for gravitational fields.
The physics of these relations is somewhat complicated. In regions of spacetime near gravitating sources, where the Riemann curvature i non-vanishing, there is failure of a principle of local energy conservation. The energy balance locally cannot be discussed independently of the coordinate one uses to calculate it, and consequently different results are obtained in various different coordinate frames — some being artifacts of the calculation itself. An amusing example of this is the case of an accelerating mass. For simplicity, let us take the mass and acceleration small, so that the deviations from Newtonian physics are small and may be treated perturbatively - the so-called post-Newtonian approximation. In this approximation the theory i similar to electromagnetic theory. In electromagnetic theory, an accelerating charge radiates and there is the radiation reaction force which tends to decelerate it; there is energy loss to the radiation field. In Einstein gravity, the accel erating mass is a source of gravitational radiation and one may calculate the radiation reaction force as one does in electromagnetic theory. A naive calculation along these lines yields a radiation reaction force term (å term in the equation of motion with a the acceleration) that ha the opposite sign to the electromagnetic case; the particle appears to speed up gaining energy as it radiates! This is an unphysical radiation reaction force. The calculation is not gauge invariant and depends on the choice of coordinate used to describe the motion of the particle.
However, though local energy conservation fails, there is a large scale principle of energy-momentum conservation in the general theory. The problem in principle was solved by Noether. She pointed out in I.V. that it is possible to construct a divergence-free quantity now generally referred to as the energy-momentum pseudotensor T mu nu eff. Jackiw et al. [21] have recently constructed such a pseudotensor using the methods of Noether introduced in her theorem II. Other constructions have been made by Weinberg [22] and Landau and Lifshitz [20]. Such pseudotensors have the form
|
| (12) |
and satisfy
|
| (13) |
The tmu nu are not unique, and they are gauge dependent. Owing to this gauge dependence, Tmu nueff is called a pseudotensor because it does not transform as a second rank tensor under the full group of general coordinate transformations. However, these constructions are covariant under the linear transformations of the Poincaré group and may be used to calculate energy and momentum in gravitationally field free regions and asymptotically field free regions. Using such pseudotensors, one can formulate a principle of energy conservation by integrating over a large, asymptotically flat spacelike hypersurface.11 In so doing one obtains a total energy-momentum four-vector Palpha which includes the energy and momentum carried by gravitational radiation and is constant in time. The tmu nu contributions take gravitational radiation into account, and the calculations are done over distances large compared to the wavelength of the radiation. This total energy-momentum vector behaves as a special relativistic four-vector for any transformation which is a Lorentz transformation far from sources and the vector is independent of the choice of coordinates used in the calculation. [19] Such a calculation is applied to the observed decrease of the orbital period of the binary pulsar PSR 1913+1916, and used to estimate the associated flux of gravitational radiation.12
The main results ofI.V.. are two theorems which are proved along with their converses. They will be described here. Felix Klein' statements [16] of the theorems are given in Appendix B.
Though they apply more generally, we shall describe the theorems as they apply to field theories. Consider an integral I over independent variables x of a functional L depending on functions (field variables) of these x variables phi(x) and their derivatives; viz.,
|
| (14) |
The functional L may also depend directly on the x. The integral I in physics is the action in the sense of Hamilton's Principle, and the functional L is the Langrangian of the theory. The theorems apply to systems for which I is an invariant of a Lie group of transformations which transform, x -> y, phi -> chi ,... ; i.e., when one ha
|
| (15) |
integrated over an arbitrary region of x space and the corresponding y space.
The two cases of a finite and an infinite Lie group are separately considered. In Noether's notation, a finite Lie group is denoted by Grho; it is a continuous group of transformations whose most general transformation depends analytically on a finite (or countably infinite) number rho of independent parameters. An infinite Lie group, on the other hand, is denoted by Ginfinity-rho. It is a continuou group whose most general transformation depends on rho independent, arbitrary functions and their derivatives. The results of theorem I apply when the action I is an invariant of a finite Lie group, and the results of theorem II when it is an invariant of an infinite Lie group. The results are different in the two cases.
Theorem I for Grho gives the result that there is a divergence for each of the rho independent generators of the group which is proportional to a Lagrange function. In her terminology the Lagrange functions of the theory are the left hand side of equations of motion (field equations) of which the right hand side vanishes. Thus when the equations of motion are satisfied, the divergences vanish. For the spacetime displacement of the Poincaré group, the four divergences are four tensor component divergences. The vanishing of these divergences give energy-momentum conservation. The U(1) Lie group of global gauge transformations in electrodynamics is another example. Corresponding to the generator of thi group, one has a divergence free current and from this one proves charge conservation.13
Theorem II applies when the action is an invariant of an infinite Lie group. The statement of the theorem for this case is very general and, aside from its application to general relativity, it applies in a wide variety of other cases. For example, quantum chromodynamics and other gauge field theories are theories to which it applies. From theorem II, one ha identities beteen Lagrange functions and their derivatives. See Appendix B. These identities Noether calls ‘dependencies’. Generally they are covariant with respect to the group. For example, the Bianchi identities in the general theory of relativity are examples of such ‘dependencies’.
It is important to point out that in I.V. proofs are given for the converses of theorems I and II as well. For example, theorem I states that if the action I is an invariant of a finite Lie group, there are rho divergences which vanish when the equations of motion are satisfied. The converse also is proved I.V..; namely that the rho vanishing divergences imply that the action is an invariant of. This result wa important in the history of discovery of symmetries in elementary particle physics. [2]
I conclude this talk with a quotation from I.V. where Noether says that Theorem II is "proof of a Hilbertian assertion about the connection of the failure of proper laws of conservation of energy with general relativity ... in a generalized group theory version." One of the reasons why her theorems have been very important for 20th century physics i because they are in ‘a generalized group theory version‘.
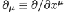is used also.
I would like to thank Mina Teicher and her colleagues for organizing this very interesting and rewarding Symposium; and my colleague Basil Gordon for the help he afforded me in understanding and appreciating the workings of the minds of these great mathematicians, and for his English translations of their papers, and for his close reading of this manuscript in its various drafts. I would also like to thank my colleague Aaron Grant for a critical reading of the final draft.
"I presented the main theorems of Frl. Noether at the July 26 meeting ... The main theorem given in section 2 above is a special case of the following far-reaching theorem of Frl. Noether:
If an integral I is invariant under a continuous group Grho with rho parameters, then rho linearly independent combinations of the Lagrangian expressions arc divergences.
Concerning in particular the claim made by Hilbert [that the failure of 'proper' energy theorems was characteristic of the theory], the following is an exact formulation according to Frl. Noether:
If an integral I is invariant under the translation group, the energy relations are improper if and only if I is invariant under an infinite-dimensional group which contains the translation group as a subgroup.
Incidentally, the theorem of Hilbert that there are four relations between the field equations [Bianchi identities] also finds its generalization in Frl. Noether's work. Her theorem is as follows:
If an integral I is invariant under a group with p arbitrary functions in it with their derivatives up to the s'th order, then there are rho identities between the Lagrangian expressions and their derivatives of order up to s."
English translation courtesy of Basil Gordon.
